Tam giác (chữ Hán: 三角, nghĩa: ba góc) hay hình tam giác là một loại hình cơ bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng. Tam giác là đa giác có số cạnh ít nhất.
Tam giác luôn luôn là đa giác đơn, lồi
[sửa]Các yếu tố trong tam giác
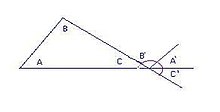
Một tam giác có ba cạnh, ba cạnh ấy tạo thành ba góc, chúng còn được gọi là các góc trong để phân biệt với các góc ngoài là góc kề bù với chúng tạo bởi một cạnh và một cạnh kéo dài.
- Trong hình bên A' là góc đối của A đã dịch chuyển, B' là góc đối của B đã dịch chuyển
Đoạn thẳng nối một đỉnh vớihình chiếu vuông góc của nó trên cạnh đối diện được gọi làđường cao của tam giác. Một tam giác có ba đường cao. Ba đường cao của một tam giác cắt nhau tại một điểm, điểm này được gọi là trực tâm của tam giác
Đoạn thẳng nối mỗi đỉnh với trung điểm của cạnh đối diện được gọi là trung tuyến của tam giác, một tam giác có ba đường trung tuyến. Ba đường trung tuyến của một tam giác cắt nhau tại một điểm, điểm này được gọi là trọng tâm của tam giác.
- Trong mặt phẳng, mọi đường thẳng đi qua một đỉnh và trọng tâm của tam giác đều chia tam giác thành hai phần có diện tích bằng nhau
Ngoài ra ba đường trung trực của ba cạnh cắt nhau tại một điểm, đó là tâm đường tròn ngoại tiếp của tam giác.
Ba đường phân giác của ba góc trong cắt nhau tại một điểm, điểm này là tâm đường tròn nội tiếp tam giác.
- Tâm đường tròn nội tiếp tam giác thì cách đều ba cạnh của tam giác
[sửa]Quan hệ bằng nhau giữa các tam giác
Hai tam giác là bằng nhau nếu chúng có thể đặt trùng khít lên nhau sau một số phép tịnh tiến, quayvà đối xứng. Nói cách khác hai tam giác là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc đối diện với các cạnh tương ứng bằng nhau. Hai tam giác bằng nhau khi và chỉ khi thỏa một trong ba điều kiện sau:
- Hai tam giác có ba cặp cạnh tương ứng bằng nhau thì bằng nhau (cạnh-cạnh-cạnh).
- Hai tam giác có hai cặp cạnh tương ứng bằng nhau và cặp góc xen giữa các cạnh đó bằng nhau thì bằng nhau (cạnh-góc-cạnh).
- Hai tam giác có một cặp cạnh bằng nhau và hai cặp góc kề với cặp cạnh ấy bằng nhau thì bằng nhau (góc-cạnh-góc).
- Trong tam giác cân hai đường tròn nội tiếp và ngoại tiếp đồng tâm với nhau.
[sửa]Quan hệ đồng dạng giữa các tam giác
Hai tam giác được gọi là đồng dạng nếu một trong chúng bằng với một tam giác nhận được từ tam giác kia sau một phép vị tự. Các điều kiện cần và đủ để hai tam giác đồng dạng:
- Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng.
- Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng.
- Hai tam giác có hai cặp cạnh tương ứng tỷ lệ, hai góc kẹp giữa hai cặp cạnh ấy bằng nhau thì đồng dạng.
Các tính chất khác:
- Tỉ số hai đường phân giác, hai đường cao, hai đường trung tuyến, hai bán kính nội tiếp vàngoại tiếp, hai chu vi tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số diện tích của hai tam giác đồng dạng thì bằng bình phương tỉ số đồng dạng.
[sửa]Phân loại tam giác
Trong hình học Euclid thuật ngữ "tam giác" thường được hiểu là tam giác nằm trong một mặt phẳng. Ngoài ra còn có tam giác cầu trong hình học cầu, tam giác hyperbol trong hình học hyperbol. Tam giác phẳng có một số dạng đặc biệt, xét theo tính chất các cạnh và các góc của nó:
- Trong tam giác thường, mọi cạnh có độ dài khác nhau, mọi góc trong cũng khác nhau.
- Tam giác đều là tam giác có cả ba cạnh có độ dài bằng nhau, nói cách khác: ba góc trong bằng nhau và
có giá trị bằng 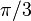 rad.
rad.
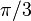 rad.
rad.- Tam giác cân là tam giác có hai cạnh có độ dài bằng nhau, các cạnh này được gọi là cạnh bên, nói cách khác: tam giác cân là tam giác có hai góc trong bằng nhau (chúng được gọi là các góc ở đáy).
 | 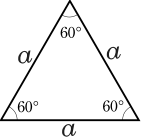 | 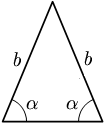 |
| Tam giác thường | Tam giác đều | Tam giác cân |
- Tam giác vuông là tam giác có một góc bằng
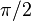 rad, góc vuông. Trong một tam giác vuông, cạnh đối diện với góc vuông gọi là cạnh huyền, là cạnh lớn nhất. Hai cạnh kia là cạnh góc vuôngcủa tam giác vuông. Định lý Pytago là định lí nổi tiếng đối với hình tam giác vuông, mang tên nhà toán học, triết gia Pytago.
rad, góc vuông. Trong một tam giác vuông, cạnh đối diện với góc vuông gọi là cạnh huyền, là cạnh lớn nhất. Hai cạnh kia là cạnh góc vuôngcủa tam giác vuông. Định lý Pytago là định lí nổi tiếng đối với hình tam giác vuông, mang tên nhà toán học, triết gia Pytago.
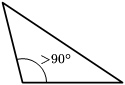
- Tam giác tù là tam giác có một góc trong lớn hơn
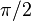 rad (một góc tù).
rad (một góc tù).
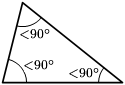
- Tam giác nhọn là tam giác có ba góc trong đều nhỏ hơn
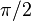 rad (ba góc nhọn).
rad (ba góc nhọn).
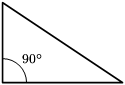 |  |  |
| Tam giác vuông | Tam giác tù | Tam giác nhọn |
- Một số tam giác khác là trường hợp đặc biệt trong các phân lớp kể trên. Thí dụ: Tam giác vuông cân vừa là tam giác vuông vừa là tam giác cân.
[sửa]Một số tính chất của tam giác (trong hình học Euclide)
- Tổng các góc trong của một tam giác bằng hai góc vuông (
 rad hay
rad hay  ).
). - Độ dài mỗi cạnh lớn hơn hiệu độ dài hai cạnh kia và nhỏ hơn tổng độ dài của chúng.
- Ba đường cao của tam giác cắt nhau tại một điểm được gọi là trực tâm của tam giác.
- Ba đường trung tuyến của tam giác cắt nhau tại một điểm được gọi là trọng tâm của tam giác. Mọi đường thẳng đi qua trọng tâm của tam giác đều chia tam giác thành hai phần có diện tích bằng nhau.
- Ba đường trung trực của tam giác cắt nhau tại một điểm là tâm đường tròn ngoại tiếp của tam giác.
- Ba đường phân giác trong của tam giác cắt nhau tại một điểm là tâm đường tròn nội tiếp của tam giác.
- Trong hai cạnh của cùng một tam giác cạnh đối diện với góc lớn hơn có chiều dài lớn hơn. Góc đối diện với cạnh lớn hơn là góc lớn hơn.
- Định lý hàm số cosin: Trong một tam giác, bình phương độ dài một cạnh bằng tổng bình phương độ dài hai canh còn lại trừ đi hai lần tích của độ dài hai cạnh ấy với cosin của góc xen giữa hai cạnh đó.
- Định lý hàm số sin: Trong một tam giác tỷ lệ giữa độ dài của mỗi cạnh với sin của góc đối diện là như nhau cho cả ba cạnh.
- Trong hình học phi Euclide thì một tam giác có thể có tổng ba góc phụ thuộc vào kích thước của tam giác, khi kích thước tam giác gia tăng thì tổng đó tiến tới giá trị là 0 và có diện tích là vô hạn.
[sửa]Các công thức tính diện tích tam giác
Tính diện tích tam giác là một bài toán sơ cấp thường gặp trong hình học sơ cấp
[sửa]Sử dụng hình học
| Diện tích S bằng S = ½bh, trong đó b là độ dài của một cạnh bất kỳ của tam giác (thường gọi làđáy) và h là độ dài đường cao hạ từ đỉnh đối diện xuống cạnh ấy.
Có thể giải thích công thức này bằng cách dùng diện tích hình chữ nhật như sau:
Từ một tam giác (màu xanh lá cây), ta sao một tam giác bằng nó,(màu xanh lam), quay góc 180°, và ghép chúng thành hình bình hành. Cắt một phần của hình bình hành, ghép lại thành hình chữ nhật. Vì diện tích hình chữ nhật là bh, nên diện tích tam giác là ½bh.
Nói cách khác, diện tích tam giác bằng độ dài cạnh đáy nhân với chiều cao chia 2:
|
[sửa]Dùng vectơ
Nếu tứ giác ABDC là hình bình hành thì diện tích của nó được tính bởi công thức:
![S_{ABCD} = |[\overrightarrow{AB},\overrightarrow{AC}]|](http://upload.wikimedia.org/math/7/6/9/769ece5689903e7e26464c658e29ff36.png)
Diện tích tam giác ABC bằng một nửa diện tích của hình bình hành ABDC nên:
![S_{ABC} = \frac{1}{2}|[\overrightarrow{AB},\overrightarrow{AC}]|](http://upload.wikimedia.org/math/2/1/c/21c13844f405df557bb29052e94dcfe7.png) |
[sửa]Dùng lượng giác
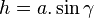 và và  nên ta có: nên ta có: |
[sửa]Dùng tọa độ
Nếu đỉnh A đặt ở gốc tọa độ (0, 0) của hệ tọa độ Descartes và tọa độ của hai đỉnh kia là B = (xB,yB) và C = (xC, yC), thì diện tích S của tam giác ABC bằng một nửa của giá trị tuyệt đối của định thức
Trong trường hợp tổng quát, ta có:
Trong không gian ba chiều, diện tích của tam giác cho bởi {A = (xA, yA, zA), B = (xB, yB, zB) và C = (xC, yC, zC)} là tổng 'Pythagor' của các diện tích các hình chiếu của chúng trên các mặt phẳng tọa độ (nghĩa là x=0, y=0 and z=0):
[sửa]Dùng công thức Heron
Cũng có thể tính diện tích tam giác S theo Công thức Heron:

trong đó  là nửa chu vi của tam giác.
là nửa chu vi của tam giác.
 là nửa chu vi của tam giác.
là nửa chu vi của tam giác.[sửa]Những nguyên tắc cơ bản
Euclid (phát âm là Ơ-clit) đã trình bày các nguyên tắc cơ bản về tam giác trong tập 1-4 tác phẩm Cơ sở (Elements) của ông, viết khoảng năm 300 TCN.
Hai tam giác là đồng dạng nếu có thể khai triển (co hay giãn) tam giác này theo cùng một tỷ lệ để có tam giác kia. Trường hợp này, độ dài của những bên đồng vị có tỷ lệ bằng nhau. Tức là nếu cạnh dài nhất trong một tam giác gấp đôi cạnh dài nhất của tam giác đồng dạng, thì cạnh ngắn nhất của nó cũng gấp đôi cạnh ngắn nhất của tam giác kia, và đường trung tuyến của tam giác đó cũng sẽ phải gấp đôi đường tương ứng của tam giác kia. Hơn nữa, tỷ lệ cạnh dài trên cạnh ngắn của một tam giác sẽ phải bằng tỷ lệ cạnh dài trên cạnh ngắn của tam giác kia. Điều quan trọng là những góc đồng vị phải bằng nhau để hai tam giác được đồng dạng nhau. Việc này cũng xảy ra nếu một tam giác có một cạnh chung với tam giác kia, và những cạnh đối với nó thì bằng nhau.
Hàm lượng giác sin và cosin có thể hiểu được khi dùng tam giác vuông và khái niệm đồng dạng. Đó là hai hàm của góc được nghiên cứu bởi lượng giác học.
[sửa]Một số định lý
Một số định lý cổ điển liên quan đến tam giác là: Định lý Pythagore, Định lý Apollonius, Định lý Stewart, .v.v.
[sửa]Các công thức liên quan
[sửa]Xem thêm
- Tam giác Heron
- Đường cao (tam giác)
- Bất đẳng thức của Pedoe
- Bất đẳng thức tam giác
- Tam giác cầu
- Tam giác Bermuda
"Theo Bách khoa toàn thư mở Wikipedia"









![[\overrightarrow{AB},\overrightarrow{AC}]](http://upload.wikimedia.org/math/c/b/8/cb81ce9f256e5306fc3c62171817fa67.png) là
là 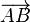 và
và  .
.
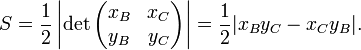


Không có nhận xét nào:
Đăng nhận xét